RNN教程4-实现GRU/LSTM网络

这是RNN教程的第四部分，也是最后一部分。我们将讨论两个RNN模型的变种—LSTM（Long Short Term Memory）和GRU（Gated Recurrent Units）。

RNN翻译教程目录：

RNN教程1-RNN的基本介绍

RNN教程2-用python、numpy和theano实现RNN

RNN教程3-BPTT算法以及消失的梯度

RNN教程4-实现GRU/LSTM网络

英文出处

关于lstm，有一篇不错的教程：http://colah.github.io/posts/2015-08-Understanding-LSTMs/

这是LSTM模型提出的原始论文《LSTM can solve hard long time lag problems
》，作者是S Hochreiter和 J Schmidhuber，这个模型也是在NLP领域里面应用的最广的一个。

而GRU则是在2014年被提出来，《Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation》，是LSTM的一个简单变体，他们有许多相同的属性。

我们先从LSTM开始，然后再看看GRU有什么不同。

LSTM网络

在RNN教程第三部分，我们提到了梯度消失的问题，也正是这个问题，导致了RNN无法学习长期依赖。LSTM就是用来解决这个问题的，因为它引入了一个叫做“门”（gating）的机制。为了搞明白这个门是什么，我们先看看LSTM是怎么计算隐藏层st的：

上面的这些式子看上去好像挺复杂的，但它没你想象的那么难。首先，我们需要注意到，LSTM层只是计算隐藏层的另一种方式。

在之前，也就是原始的RNN，我们用 $s_{t}=\tanh(Ux_{t}+Ws_{t-1})$ 这个式子来计算隐藏层，隐藏层的输入单元有两个，一个是当前时间步的输入 $x_{t}$ ，另一个是上一个隐藏状态 $s_{t-1}$ 。LSTM单元干的也是一样的事情，只不过换了个方式而已！这是理解LSTM的关键。现在，你最终可以把LSTM和GRU当作一个黑盒来使用，只要给你一个当前时间的输入以及上一个状态，你就可以计算出下一个状态了。正如下图：

有了这样的铺垫之后，我们就可以来看看LSTM的隐藏层是怎么来计算的了。Chris Olah有一篇博文介绍的很清楚（http://colah.github.io/posts/2015-08-Understanding-LSTMs/），为了不做重复工作，我在这里会给出比较简洁的解释。当然，想要理解更深刻一些，我建议你还是去拜读一下他的那篇博客。好了，我们开始吧。

i，f，o分别被称为input（输入）门，forget（遗忘）门和输出（output）门。注意，他们有着相同结构的等式，只不过参数是不一样的。他们之所以被称为门，是因为sigmoid函数会将这些向量映射到0到1这个区间，然后拿它们和其它的向量相乘，你就能决定究竟让多少其它的向量“通过”这个门。输入门能让你决定放多少当前时间步新计算的信息通过，遗忘门能让你决定放多少上个状态的信息通过，最后的输出门能让你决定放多少信息给到更高一层神经网络或者下一个时间步。这三个门都有同样的维度ds，也就是隐藏层的大小。
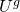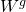g是基于当前输入和先前隐藏状态计算的“候选”隐藏状态。这个式子和我们在原始RNN中的式子是一样的，我们只是把参数U,W改成了 $U^{g}$ 和 $W^{g}$ 而已。在原始RNN中，我们是直接把g的值当作一个状态输出给下一个状态，在LSTM中，我们将用输入门来挑选g的一部分值，再输出给下一个状态。
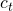$c_{t}$ 就是内部的记忆单元了。它是上一个记忆单元和遗忘门相乘的结果，再加上隐藏候选状态g和输入门相乘的结果。这样，我们既可以完全忘记上一个记忆单元的内容（把遗忘门全部置为0），也可以完全忽略掉新的输入状态（把输入门全部置为0），当然现实情况是我们需要的结果是这两种极端情况之间。
给定了记忆单元 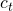$c_{t}$ ，我们最终要计算出隐藏状态 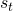$s_{t}$ ，由式子可知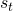， $s_{t}$ 是由输出门和记忆单元（用tanh处理）相乘得到的。并非所有的内部记忆单元都与其他隐藏状态相关。

下面是出自《Empirical evaluation of gated recurrent neural networks on sequence modeling》这篇论文的一张图，描述LSTM的内部细节：

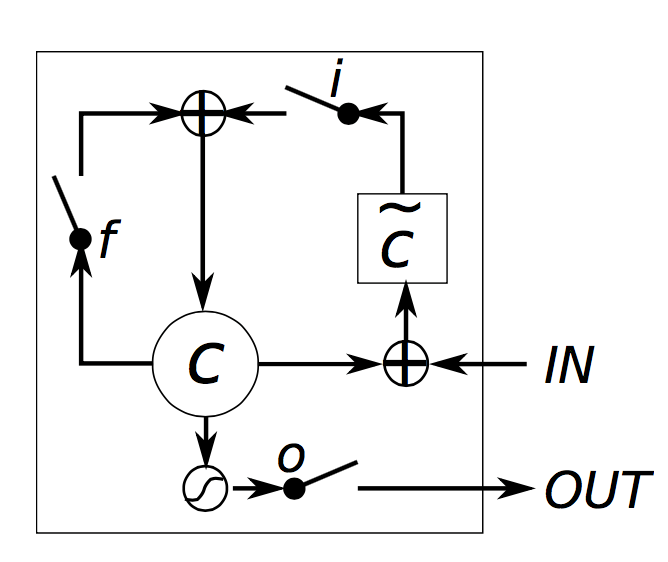
直观上来看，原始的RNN似乎可以看作是LSTM的一个特例—当你将输入门全部置为1，、遗忘门全部置为0（你总是忽略之前的记忆单元）、输出门全部置为1，你就会几乎得到标准的RNN，只不过多了个tanh压缩了一下输出。正是这个“门机制”让LSTM能够明确的建立长期记忆依赖，通过学习这些门的参数，神经网络能够更好的利用这些记忆。

要注意的是，LSTM的结构也有几种变种。一个最常见的变种就是创建peephole（窥见孔），这个peephole能让门不仅仅依赖于上一个状态 $s_{t-1}$ ，也依赖于上一个内部记忆单元 $c_{t-1}$ 。在门方程增加附选项即可。这篇论文（LSTM: A Search Space Odyssey）评估了不同的lstm结构。

GRU网络

GRU网络背后的思想和LSTM非常相似，它的式子如下：

GRU中有两个门，重置（reset）门r和更新（update）门z。从直观上看，重置门决定了新的输入和上一个记忆怎么组合，更新门决定了保留多少前面的记忆信息。如果我们把重置门全部置为1，更新门全部置为0，我们就又重新得到原始的RNN模型了。它的思想和LSTM是一致的，都是用门机制来学习长期记忆以来，但是它有几个关键的区别：

GRU有两个门，LSTM有3个。
GRU没有内部记忆单元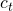（ $c_{t}$ ），也没有LSTM中中的输出门。
LSTM的输入门和遗忘门，在GRU中被整合成一个更新门z；而重置门r被直接用到前一个隐藏状态上面了。因此，LSTM中重置门的职责实际上被分为GRU中的r和z。
计算输出的时候，我们不会再多用一次非线性的变换了。

下面是出自《Empirical evaluation of gated recurrent neural networks on sequence modeling》这篇论文的一张图，描述GRU的内部细节：

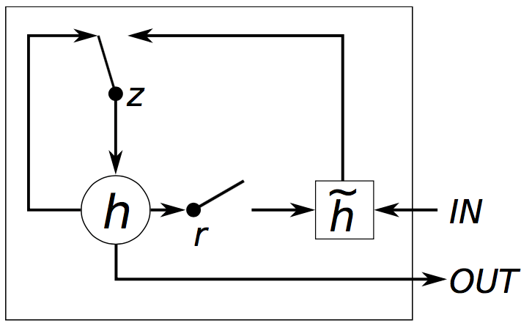
GRU和LSTM的对比

现在你已经见识到这两个为了解决RNN梯度消失问题而提出的模型了，你也可能会好奇：我该用哪个？GRU是比较新的模型（2014年提出的），关于它的一些利弊现在还没有探索清楚。从这两篇论文来看： Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 和 An Empirical Exploration of Recurrent Network Architectures，两个模型难以分出胜负。在许多任务里面，这两个模型有不同的表现，然而，更多情况下，调整超参数会比选择模型更重要。

GRU有更少的参数（U、W规模比较小），所以训练起来会更快一些，而且需要的训练数据也少一些。相对应的，如果你有足够的训练数据，LSTM会是更好的选择。

实现

让我们回顾一下RNN教程第2部分提到的语言模型，这次，我们用GRU来实现。（LSTM的实现也差不多，只不过式子不一样而已）

我们通过之前theano版本的代码来修改，还是要记住这一点，GRU（或者LSTM）层只是换了一种方式计算隐藏层而已。所以，我们需要做的，仅仅是在前向转播的代码里，把隐藏层的计算步骤修改一下。

def forward_prop_step(x_t, s_t1_prev):
      # This is how we calculated the hidden state in a simple RNN. No longer!
      # s_t = T.tanh(U[:,x_t] + W.dot(s_t1_prev))
       
      # Get the word vector
      x_e = E[:,x_t]
       
      # GRU Layer
      z_t1 = T.nnet.hard_sigmoid(U[0].dot(x_e) + W[0].dot(s_t1_prev) + b[0])
      r_t1 = T.nnet.hard_sigmoid(U[1].dot(x_e) + W[1].dot(s_t1_prev) + b[1])
      c_t1 = T.tanh(U[2].dot(x_e) + W[2].dot(s_t1_prev * r_t1) + b[2])
      s_t1 = (T.ones_like(z_t1) - z_t1) * c_t1 + z_t1 * s_t1_prev
       
      # Final output calculation
      # Theano's softmax returns a matrix with one row, we only need the row
      o_t = T.nnet.softmax(V.dot(s_t1) + c)[0]
 
      return [o_t, s_t1]

在我们的实现代码里面，我们添加了偏置单元b、c，这在之前的等式里面没有体现。当然我们也要更改U、W的初始化，因为我们现在有这不同的大小了，在这里代码就不贴出来了，在github（https://github.com/dennybritz/rnn-tutorial-gru-lstm）上面有，我还加了一个word embedding层E。

这很简单，但是梯度怎么办？我们仍然可以跟以前一样应用链式求导法则，但实际上，更多人用一些库来完成这个步骤，比如theano。如果你还是想自己动手计算梯度，你可能需要实现不同模块的求导算法。在这里，我们让theano直接帮我们计算：

# Gradients using Theano
dE = T.grad(cost, E)
dU = T.grad(cost, U)
dW = T.grad(cost, W)
db = T.grad(cost, b)
dV = T.grad(cost, V)
dc = T.grad(cost, c)

很好！为了得到更好的结果，我们使用了一些小技巧。下面就来说说看。

使用rmsprop来进行参数的更新

在RNN教程第二部分，我们使用了最基本的SGD算法来进行参数的更新，然而它表现的并不是那么好。如果你把学习率设置得很低，SGD确实会让你得到好的训练效果，但是这样就太慢了。为了解决这个问题，有很多SGD算法的变种，包括 (Nesterov) Momentum Method）, AdaGrad, AdaDelta 和 rmsprop，这里有一篇文章总结得很好（http://cs231n.github.io/neural-networks-3/#update）。

在这部分教程，我将使用rmsprop这个方法，它背后的思想是：根据先前的梯度和来调整每个参数的学习率。直观上我们可以这么理解，就是频繁出现的特征获得较小的学习率（因为他们的梯度总和更大），而比较少出现的特征就获得更大的学习率。

Rmsprop算法的实现非常简单，对于每一个参数，我们对应存储一个缓存变量，在梯度下降的过程中我们更新参数以及缓存变量，正如下式（以W为例）：

cacheW = decay * cacheW + (1 - decay) * dW ** 2
W = W - learning_rate * dW / np.sqrt(cacheW + 1e-6)

衰减率设置在0.9到0.95之间，另外1e-6是为了避免分母为0

添加embedding层

使用word embedding（词嵌入）层是改进模型精确度的流行方法，其中word2vec和GloVe都是比较出名的。和用one-hot表示句子不同，这种词嵌入的方法用低维（通常是几百维）的向量来表示词语，这有个好处，那就是能通过向量来判断两个词的语义是否相近，因为如果他们意思相近的话，他们的向量就很相近。要使用这些向量，需要预训练语料库。从直觉上来看，使用word embedding层，就相当于你告诉神经网络词语的意思，从而神经网络就不需要学习关于这些词语的知识了。

增加第二个GRU层

为我们的神经网络增加多一层，能够使得模型捕捉更高层次的交互信息，你可以加多几层，但我对这个实验并没有做过多的尝试。你可能在2，3层的计算之后，发现计算值逐渐减小，而且如果你没有足够的数据，增加层数是没有效果的，另外可能造成过拟合。

增加一层GRU或者LSTM是很简单的，我们只需要修改前向传播的计算过程以及初始化函数：

# GRU Layer 1
z_t1 = T.nnet.hard_sigmoid(U[0].dot(x_e) + W[0].dot(s_t1_prev) + b[0])
r_t1 = T.nnet.hard_sigmoid(U[1].dot(x_e) + W[1].dot(s_t1_prev) + b[1])
c_t1 = T.tanh(U[2].dot(x_e) + W[2].dot(s_t1_prev * r_t1) + b[2])
s_t1 = (T.ones_like(z_t1) - z_t1) * c_t1 + z_t1 * s_t1_prev
 
# GRU Layer 2
z_t2 = T.nnet.hard_sigmoid(U[3].dot(s_t1) + W[3].dot(s_t2_prev) + b[3])
r_t2 = T.nnet.hard_sigmoid(U[4].dot(s_t1) + W[4].dot(s_t2_prev) + b[4])
c_t2 = T.tanh(U[5].dot(s_t1) + W[5].dot(s_t2_prev * r_t2) + b[5])
s_t2 = (T.ones_like(z_t2) - z_t2) * c_t2 + z_t2 * s_t2_prev

最后，完整代码戳这里：https://github.com/dennybritz/rnn-tutorial-gru-lstm/blob/master/gru_theano.py

关于RNN教程，就翻译到这里了，过程中有修改、删除部分内容，有什么问题可以评论里一起探讨，谢谢！